本课的核心是教你如何使用克里金法,特别是普通克里金法,来创建一个比简单反距离加权法更精确、更可靠的网格。
教程11:克里金法入门
本课目标
- 理解克里金法的基本概念:了解它是什么,以及为什么它比其他插值方法(如 IDW)更高级。
- 掌握普通克里金法的应用:学会在 Surfer 中使用普通克里金法创建网格。
- 分析克里金法生成的结果:学会解读克里金法生成的网格图、等高线图以及最重要的 误差/方差图。
- 比较不同插值方法:对比克里金法与反距离加权法 的结果差异。
核心概念解析
在开始操作前,我们先理解几个关键术语,这会让你事半功倍。
什么是克里金法?
克里金法是一种先进的插值技术,源自地质统计学,它的核心思想不仅仅是简单地根据周围点进行平均,而是:
- 考虑空间相关性:它假设距离较近的采样点比距离较远的采样点更相似,这种相关性由一个叫做半变异函数 的工具来量化。
- 提供误差估计:这是克里金法最强大的特点之一,它在估算未知点值的同时,会给出这个估算值的不确定性或可靠性,换句话说,它告诉你“我对这个点的估算有多大把握?”。
半变异函数
这是克里金法的“引擎”,你可以把它想象成一个工具,用来衡量数据点之间的“差异”如何随距离变化。
- 块金效应:当距离为零时,理论上半方差值也应为零,但在实际中,即使同一个位置多次测量也会有差异,或者存在微观尺度的变化,这个在零距离处的非零值就是块金效应,代表了测量误差和微观变异。
- 基台值:当距离足够大时,数据点之间不再相关,半方差会趋近于一个稳定的最大值,这个值就是基台值,它代表了整个研究区域的总变异。
- 变程:当两个点的距离达到这个值时,它们在空间上不再相关,变程决定了每个采样点影响的“半径”。
简单比喻:想象你在听一个嘈杂房间里的声音,离你很近的人(小距离),你能听清他们的声音(差异小),离你很远的人(大距离),他们的声音和背景噪音混在一起,你无法分辨(差异大),半变异函数就是描述这种“声音清晰度”如何随距离变化的数学模型。
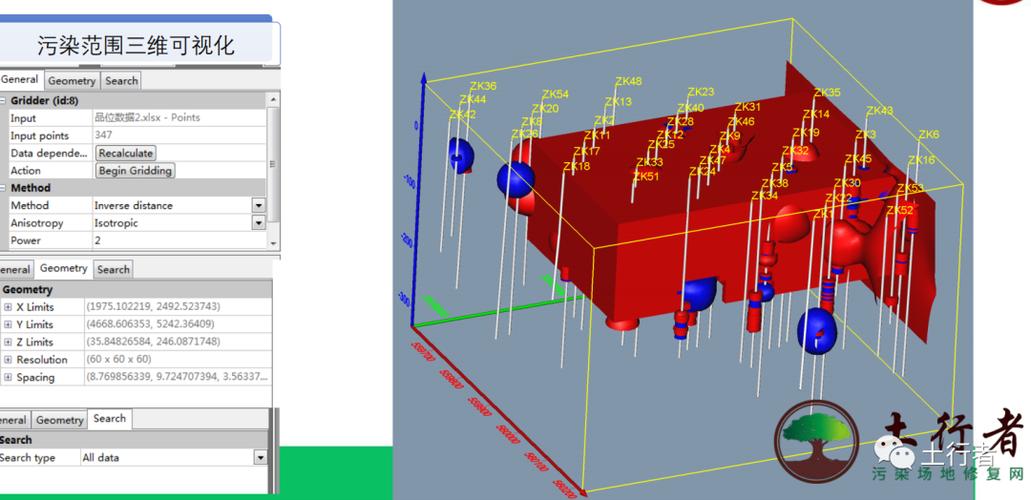
普通克里金法
这是最常用、最基础的克里金法,它假设在研究区域内,任意位置的未知值都是一个常数(均值)加上一个随机的、与空间位置相关的误差项,它不对数据的整体趋势(如趋势面)进行建模,只关注局部的空间相关性。
操作步骤详解
假设我们已经有了教程数据,通常是一系列带有 X, Y, Z 坐标的点数据文件(elev_pts.dat)。
使用普通克里金法创建网格
- 启动 Surfer,并打开工作区。
- 在菜单栏选择 网格 -> 数据...。
- 在弹出的“网格化数据”对话框中:
- 选择你的数据文件(
elev_pts.dat)。 - 关键一步:在“网格化方法”的下拉菜单中,选择 克里金法。
- 点击 高级... 按钮,这是进入克里金法核心参数的地方。
- 选择你的数据文件(
- 设置克里金法高级选项:
- 克里金类型:选择 普通。
- 半变异函数模型:Surfer 会根据你的数据自动拟合一个模型,你可以看到它选择的模型(如球状模型、指数模型、高斯模型)以及拟合的参数(块金、基台、变程),你可以手动调整这些参数来获得更好的拟合,但通常自动拟合的结果已经很不错了。
- 搜索半径:设置在估算每个网格节点时,要考虑的周围数据点的最大距离,你可以设置一个固定值,或者让程序自动计算。
- 点击 确定,返回到“网格化数据”主对话框。
- 设置网格化选项:你可以像往常一样设置网格的线数、X/Y 范围等。
- 点击 确定,Surfer 将开始使用克里金法计算网格文件,这个过程可能比 IDW 稍慢,因为它在计算半变异函数。
可视化克里金法的结果
克里金法不仅仅是生成一个网格文件,更重要的是它生成了一个包含方差信息的网格文件,这个文件通常比普通网格文件大一倍,因为它存储了每个点的估算值和对应的方差。
-
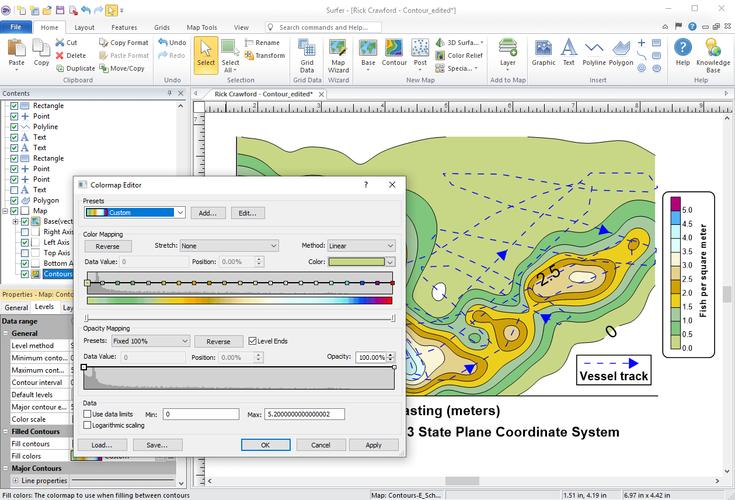
绘制等高线图/网格图:
 (图片来源网络,侵删)
(图片来源网络,侵删)- 使用新创建的克里金法网格文件(
elev_krig.grd)。 - 绘制等高线图或彩色网格图,你会发现,相比 IDW,克里金法生成的表面通常更平滑,尤其是在数据点稀疏的区域。
- 使用新创建的克里金法网格文件(
-
绘制误差/方差图(最重要的步骤!):
- 关键操作:在“映射”菜单中,选择 新建等高线图 或 新建网格图。
- 在选择文件时,不要选择主网格文件,而是选择那个包含方差信息的网格文件,它的文件名通常会是
elev_krig_var.grd或者类似的(取决于你的设置)。 - 将这个方差图用一种不同的方式显示,
- 使用灰度色阶,因为方差是正值。
- 将其叠加在主网格图的下方,作为底图。
- 解读方差图:
- 低方差区域(深色):表示这些位置的估算结果非常可靠,通常这些区域靠近原始数据点。
- 高方差区域(浅色/白色):表示这些位置的估算结果不确定性很高,通常这些区域位于原始数据点的中间,或者远离任何数据点的边缘。
方差图是克里金法的精髓! 它告诉你这张地图的哪些部分可以信任,哪些部分需要谨慎对待,甚至需要补充更多的数据。
克里金法 vs. 反距离加权法
| 特性 | 克里金法 | 反距离加权法 |
|---|---|---|
| 理论基础 | 基于统计和空间相关性,理论更严谨。 | 基于简单的几何距离,直观易懂。 |
| 输出结果 | 除了估算值,还提供方差/误差图。 | 只提供估算值,无法评估不确定性。 |
| 平滑度 | 生成的表面通常更平滑,尤其是在数据稀疏区。 | 在数据点处会形成“牛眼”效应,不够平滑。 |
| 权重计算 | 基于半变异函数,不仅考虑距离,还考虑数据的空间结构。 | 仅根据距离的幂次方计算,距离越近权重越大。 |
| 适用性 | 适用于大多数科学领域,特别是需要评估不确定性的情况。 | 适用于数据点分布均匀、且不需要误差估计的快速制图。 |
总结与提示
- 何时使用克里金法? 当你的数据点分布不均匀,或者你需要科学地评估你生成的地图的可靠性时,克里金法是首选。
- 半变异函数是关键:花点时间理解并观察半变异函数的拟合情况,一个好的拟合是高质量克里金网格的基础。
- 永远查看方差图:不要只看最终的等高线图或网格图,一定要生成并分析方差图,它才是克里金法赋予你的“超能力”。
- 练习:尝试用同一组数据,分别用 IDW 和克里金法生成网格,然后对比它们的等高线图和克里金法的方差图,你会对两者的差异有一个直观的认识。
通过这节课的学习,你已经掌握了 Surfer 中最强大的插值工具之一,能够生成更科学、更专业的空间数据模型,恭喜你!