数据结构与算法分析(Java)答案解析:从理论到实践,攻克编程难关 面对浩如烟海的“数据结构与算法分析(Java)”习题,你是否感到迷茫?本文不仅提供常见问题的答案,更注重深入解析背后的思想与实现技巧,帮助你真正理解数据结构与算法的精髓,提升Java编程能力,轻松应对面试与实战挑战。

引言:为什么“数据结构与算法分析(Java)”如此重要,我们又为何需要“答案”?
“数据结构与算法分析(Java)”是计算机科学领域的基石,也是每一位Java程序员进阶的必经之路,它不仅关乎程序的效率与性能,更是培养逻辑思维、问题解决能力的关键,这门课程的学习曲线往往较为陡峭,大量的习题和复杂的实现常常让初学者望而生畏。
当我们在百度搜索“数据结构与算法分析java 答案”时,我们真正需要的可能不仅仅是几个孤立的答案,我们渴望的是:
- 验证思路: 确保自己的解法是正确的。
- 启发思路: 当自己卡壳时,获得新的解题灵感。
- 深化理解: 从答案中学习更优的实现方式和底层原理。
- 查漏补缺: 通过对比发现知识盲点。
本文将摒弃简单的答案罗列,采用“问题引入 + 思路解析 + Java代码实现 + 复杂度分析”的模式,带你系统地攻克几个经典问题,真正实现“授人以渔”。
第一部分:线性结构——数组与链表的经典问题
线性结构是最基础的数据结构,掌握它至关重要。

问题1:如何在Java中实现一个动态数组(如ArrayList)的扩容机制?
问题引入: Java中的ArrayList为何能动态增长其容量?当我们向已满的ArrayList中添加元素时,它内部发生了什么?
思路解析: 动态数组的核心在于“扩容”,当数组元素数量达到其容量上限时,我们需要创建一个更大的新数组,然后将旧数组中的所有元素复制到新数组中,最后将新数组引用赋值给旧数组引用,这个过程称为“重新分配”(Reallocation)。
- 初始容量:
ArrayList在创建时可以指定初始容量,默认为10。 - 扩容策略: 每次扩容时,新容量通常是旧容量的1.5倍(使用位运算优化:
oldCapacity + (oldCapacity >> 1)),这种策略在空间和时间上取得了较好的平衡。 - 性能考量: 扩容和数组复制是一个O(n)时间复杂度的操作,但由于分摊分析(Amortized Analysis),向
ArrayList中添加单个元素的平均时间复杂度仍为O(1)。
Java代码实现(简化版):
import java.util.Arrays;
public class MyArrayList<T> {
private Object[] elementData;
private int size;
public MyArrayList() {
this(10); // 默认初始容量为10
}
public MyArrayList(int initialCapacity) {
if (initialCapacity < 0) {
throw new IllegalArgumentException("Illegal Capacity: " + initialCapacity);
}
this.elementData = new Object[initialCapacity];
}
public void add(T element) {
// 检查是否需要扩容
ensureCapacityInternal(size + 1);
// 添加元素
elementData[size++] = element;
}
private void ensureCapacityInternal(int minCapacity) {
// 如果是第一次添加,容量为默认值
if (elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
minCapacity = Math.max(DEFAULT_CAPACITY, minCapacity);
}
// 如果所需最小容量大于当前数组长度,则扩容
if (minCapacity - elementData.length > 0) {
grow(minCapacity);
}
}
private static final int DEFAULT_CAPACITY = 10;
private static final Object[] DEFAULTCAPACITY_EMPTY_ELEMENTDATA = {};
private void grow(int minCapacity) {
int oldCapacity = elementData.length;
// 新容量为旧容量的1.5倍
int newCapacity = oldCapacity + (oldCapacity >> 1);
// 如果新容量仍不够,则使用所需最小容量
if (newCapacity - minCapacity < 0) {
newCapacity = minCapacity;
}
// 复制数组
elementData = Arrays.copyOf(elementData, newCapacity);
}
// ... 其他方法如get, set, remove等
}
复杂度分析:

- add(E e): 平均时间复杂度为O(1),虽然扩容时是O(n),但由于扩容频率不高,分摊到每次添加操作上,成本可以忽略。
- 空间复杂度: O(n),需要额外的空间来存储元素。
问题2:如何判断一个单链表是否有环?
问题引入: 给定一个单链表的头节点,如何判断链表中是否存在环?这是一个经典的面试题。
思路解析: 判断链表是否有环,最经典、最高效的方法是“快慢指针法”(也称为Floyd's Cycle-Finding Algorithm)。
- 定义两个指针:
slow和fast,都指向链表的头节点。 - 移动规则:
slow指针每次向前移动一步,fast指针每次向前移动两步。 - 判断逻辑:
- 如果链表没有环,
fast指针会先到达链表末尾(即fast或fast.next为null)。 - 如果链表有环,
fast指针最终一定会从后面追上slow指针(即两者指向同一个节点),因为每次fast比slow多走一步,在环中它们之间的距离会逐渐缩小,最终相遇。
- 如果链表没有环,
Java代码实现:
class ListNode {
int val;
ListNode next;
ListNode(int x) { val = x; }
}
public class LinkedListCycle {
public boolean hasCycle(ListNode head) {
if (head == null || head.next == null) {
return false;
}
ListNode slow = head;
ListNode fast = head.next;
while (slow != fast) {
if (fast == null || fast.next == null) {
return false;
}
slow = slow.next;
fast = fast.next.next;
}
return true; // 如果循环结束,说明slow和fast相遇,有环
}
}
复杂度分析:
- 时间复杂度: O(n),其中n是链表中的节点数,在最坏的情况下,我们需要遍历整个链表。
- 空间复杂度: O(1),我们只使用了两个指针,没有使用额外的存储空间。
第二部分:树结构——二叉树的遍历
二叉树是另一种核心数据结构,遍历是二叉树操作的基础。
问题3:请用Java实现二叉树的前序、中序、后序遍历(递归与非递归)
问题引入: 二叉树的遍历有四种主要方式:前序、中序、后序和层序,每种遍历的访问顺序不同,如何用Java实现它们?
思路解析: 假设二叉树节点定义如下:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
-
递归实现:
- 前序遍历 (Pre-order): 根 -> 左 -> 右
- 中序遍历 (In-order): 左 -> 根 -> 右
- 后序遍历 (Post-order): 左 -> 右 -> 根 递归的实现方式非常直观,代码简洁,完全符合访问顺序的定义。
-
非递归实现: 递归的本质是系统栈的帮助,非递归实现需要我们自己使用栈来模拟这个过程。
- 前序遍历: 使用一个栈,先将根节点入栈,然后循环执行:出栈一个节点并访问,将其右孩子、左孩子依次入栈(注意顺序,因为栈是后进先出)。
- 中序遍历: 使用一个栈,从根节点开始,一路将所有左孩子入栈,直到为空,然后出栈一个节点访问,再转向其右子树,重复上述过程。
- 后序遍历: 非递归实现相对复杂,可以使用两个栈,或者一个栈配合一个标记,一个巧妙的方法是“逆序前序遍历”:将访问顺序改为“根 -> 右 -> 左”,然后将结果反转即可得到“左 -> 右 -> 根”。
Java代码实现(以非递归为例):
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
public class BinaryTreeTraversal {
// 非递归前序遍历
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) return result;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val); // 访问根节点
if (node.right != null) {
stack.push(node.right); // 右孩子先入栈,后出栈
}
if (node.left != null) {
stack.push(node.left); // 左孩子后入栈,先出栈
}
}
return result;
}
// 非递归中序遍历
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
TreeNode curr = root;
while (curr != null || !stack.isEmpty()) {
// 一路向左,将所有左孩子入栈
while (curr != null) {
stack.push(curr);
curr = curr.left;
}
// 出栈并访问
curr = stack.pop();
result.add(curr.val);
// 转向右子树
curr = curr.right;
}
return result;
}
// 非递归后序遍历 (使用两个栈)
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) return result;
Stack<TreeNode> stack1 = new Stack<>();
Stack<TreeNode> stack2 = new Stack<>();
stack1.push(root);
while (!stack1.isEmpty()) {
TreeNode node = stack1.pop();
stack2.push(node); // 将节点按根-右-左的顺序压入stack2
if (node.left != null) {
stack1.push(node.left);
}
if (node.right != null) {
stack1.push(node.right);
}
}
// 从stack2中弹出,即为后序遍历顺序
while (!stack2.isEmpty()) {
result.add(stack2.pop().val);
}
return result;
}
}
复杂度分析:
- 时间复杂度: 所有遍历方式均为O(n),需要访问每个节点一次。
- 空间复杂度:
- 递归:O(h),其中h是树的高度,最坏情况下(树退化为链表),空间复杂度为O(n)。
- 非递归:O(h),栈中最多存储h个节点,最坏情况下也是O(n)。
第三部分:排序算法——归并排序与快速排序
排序算法是算法分析中的重头戏,理解其原理和性能至关重要。
问题4:请用Java实现归并排序和快速排序,并分析其时间复杂度和空间复杂度。
思路解析:
-
归并排序:
- 思想: 分治法,将数组不断二分,直到每个子数组只有一个元素(天然有序),然后将这些有序的子数组合并成一个大的有序数组。
- 核心操作: 合并两个有序数组,需要额外的辅助空间。
- 特点: 是一种稳定的排序算法,时间复杂度稳定,但需要O(n)的额外空间。
-
快速排序:
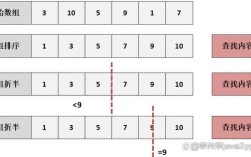
- 思想: 分治法,选择一个“基准”(pivot),将数组分区,使得基准左边的元素都小于等于基准,右边的元素都大于基准,然后递归地对左右两个子数组进行排序。
- 核心操作: 分区,原地分区,不需要额外空间(递归栈除外)。
- 特点: 平均情况下效率很高,但最坏情况下(如数组已有序)时间复杂度会退化到O(n²),是不稳定的排序算法。
Java代码实现:
import java.util.Arrays;
public class SortingAlgorithms {
// 归并排序
public static void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
}
private static void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[right - left + 1];
int i = left, j = mid + 1, k = 0;
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while (i <= mid) {
temp[k++] = arr[i++];
}
while (j <= right) {
temp[k++] = arr[j++];
}
System.arraycopy(temp, 0, arr, left, temp.length);
}
// 快速排序
public static void quickSort(int[] arr, int low, int high) {
if (low < high) {
int pivotIndex = partition(arr, low, high);
quickSort(arr, low, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, high);
}
}
private static int partition(int[] arr, int low, int high) {
int pivot = arr[high]; // 选择最后一个元素作为基准
int i = low - 1; // i是小于基准的区域的边界
for (int j = low; j < high; j++) {
if (arr[j] <= pivot) {
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high); // 将基准放到正确的位置
return i + 1;
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
int[] arr1 = {12, 11, 13, 5, 6, 7};
System.out.println("归并排序前: " + Arrays.toString(arr1));
mergeSort(arr1, 0, arr1.length - 1);
System.out.println("归并排序后: " + Arrays.toString(arr1));
int[] arr2 = {12, 11, 13, 5, 6, 7};
System.out.println("快速排序前: " + Arrays.toString(arr2));
quickSort(arr2, 0, arr2.length - 1);
System.out.println("快速排序后: " + Arrays.toString(arr2));
}
}
复杂度分析:
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 最好时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 稳定 |
| 快速排序 | O(n log n) | O(n²) | O(n log n) | O(log n) (递归栈) | 不稳定 |
超越“答案”,拥抱“理解”
回到我们最初的问题——“数据结构与算法分析java 答案”,通过以上几个经典问题的详细解析,你应该已经发现,真正的价值不在于记住答案,而在于理解每一个数据结构的设计初衷和每一种算法的精妙思想。
- 动手实践: 看懂代码不等于会写代码,一定要亲手敲一遍,尝试修改和扩展。
- 对比分析: 对于同一个问题(如排序),对比不同算法的优劣,思考它们在不同场景下的适用性。
- 触类旁通: 学会了单链表,可以思考双向链表、循环链表;学完了二叉树,可以思考二叉搜索树、AVL树、红黑树。
数据结构与算法的世界广阔而深邃,希望这篇文章能成为你探索之旅中的一盏明灯,帮助你从“寻找答案”的迷茫中走出,迈向“创造答案”的自信,持续学习,不断实践,你一定能攻克这些编程难关,成为一名优秀的Java开发者!
(文章末尾可添加相关标签,如:#数据结构 #算法 #Java #编程学习 #面试准备 #算法分析 #代码实现)