大 O 表示法

在讨论算法复杂度时,我们通常使用 大 O 表示法，它描述的是随着输入数据规模 n 的增长，算法执行时间或空间消耗的增长趋势。

• 关注点：关注最坏情况下的增长趋势，而不是具体的执行时间。
• 忽略常数：O(2n) 和 O(n) 被认为是同级的，都写作 O(n)，我们关心的是 n 的量级，而不是 2 这个系数。
• 常见复杂度从优到劣：
  • O(1) - 常数时间
  • O(log n) - 对数时间
  • O(n) - 线性时间
  • O(n log n) - 线性对数时间
  • O(n²) - 平方时间
  • O(2ⁿ) - 指数时间
  • O(n!) - 阶乘时间

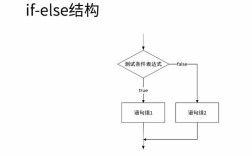
if 语句的复杂度

if 语句本身并不直接导致复杂度的增长，它的作用是程序流程控制，一个 if 语句的执行时间可以被看作是一个常数时间操作，即 O(1)。

if 语句对复杂度的影响主要体现在它是否改变了循环的执行次数。

if 语句在循环内部（不影响循环次数）

当 if 语句位于循环内部，但它只是对循环中的每个元素进行条件判断或操作，而没有改变循环总共要执行多少次时，if 语句的复杂度是 O(1)，它不会增加整个算法的复杂度。

示例：查找数组中是否存在某个元素

public boolean containsElement(int[] arr, int target) {
    // 循环会执行 n 次 (n = arr.length)
    for (int i = 0; i < arr.length; i++) {
        // if 语句本身是 O(1) 操作
        // 它在每次循环中都会执行一次
        if (arr[i] == target) {
            return true; // 找到后提前退出
        }
    }
    return false;
}

复杂度分析：

• 最好情况：目标元素在数组第一个位置。if 条件为真，循环只执行 1 次，时间复杂度为 O(1)。
• 最坏情况：目标元素在数组最后一个位置，或者不存在，循环需要执行 n 次，每次循环内部的操作（if 判断）都是 O(1)，所以总的时间复杂度是 n * O(1)，即 O(n)。
• 平均情况：通常我们讨论的是最坏情况，所以这个算法的复杂度是 O(n)。

在这个例子中,if 语句是 O(1)，而主导复杂度的是 for 循环的 n 次执行。

if 语句包裹循环（改变循环执行次数）

当 if 语句决定了一个循环是否被执行时，它会影响算法的复杂度，这通常被称为条件复杂度。

示例：根据条件决定是否进行排序

public void processData(int[] data, boolean needsSorting) {
    // if 语句是 O(1)
    if (needsSorting) {
        // 假设使用了一个 O(n log n) 的排序算法，Arrays.sort()
        // 这个循环/排序操作是 O(n log n)
        Arrays.sort(data); 
    }
    // ... 其他 O(1) 操作
}

复杂度分析：

• needsSorting 为 true：算法的主要耗时是 Arrays.sort()，时间复杂度为 O(n log n)。
• needsSorting 为 false：if 语句内的代码块不执行，算法只执行一些 O(1) 的操作，时间复杂度为 O(1)。

在这种情况下,算法的复杂度取决于输入条件，我们通常描述其最坏情况复杂度，即 O(n log n)。

for 循环的复杂度

for 循环是导致算法复杂度增长的最常见结构，它的复杂度主要取决于循环执行的次数，而这个次数通常与输入规模 n 相关。

单层 for 循环

如果循环体是 O(1) 操作，那么整个循环的复杂度就是 O(n)，n 是循环的次数。

示例：计算数组所有元素的和

public int calculateSum(int[] arr) {
    int sum = 0;
    // 循环执行 n 次 (n = arr.length)
    for (int i = 0; i < arr.length; i++) {
        // 循环体内部是 O(1) 操作 (加法、赋值)
        sum += arr[i]; 
    }
    return sum;
}

复杂度分析： 循环执行了 n 次，每次循环体内部是 O(1) 的操作，总时间复杂度为 O(n)。

嵌套 for 循环

当 for 循环内部嵌套了另一个 for 循环时，复杂度会相乘。

示例：使用冒泡排序思想查找数组中的所有重复元素

public void findDuplicates(int[] arr) {
    // 外层循环执行 n 次
    for (int i = 0; i < arr.length; i++) {
        // 内层循环对于每个 i，大约执行 n - i 次
        // 平均来看，内层循环也执行了约 n 次
        for (int j = i + 1; j < arr.length; j++) {
            // 循环体是 O(1) 操作
            if (arr[i] == arr[j]) {
                System.out.println("Found duplicate: " + arr[i]);
                break; // 找到一个即可，不影响量级
            }
        }
    }
}

复杂度分析：

• 外层循环执行 n 次。
• 对于外层循环的每一次,内层循环平均执行 n/2 次。
• 总操作次数大约是 n * (n/2)，即 n²/2。
• 根据大 O 表示法的规则，我们忽略常数 1/2，所以时间复杂度为 O(n²)。

循环次数与 n 成非正比关系

循环的次数不一定正好是 n，只要是 n 的一个线性函数（如 c*n + k），复杂度仍然是 O(n)。

示例：遍历数组的前半部分

public void printFirstHalf(int[] arr) {
    // 循环执行 n/2 次
    for (int i = 0; i < arr.length / 2; i++) {
        System.out.println(arr[i]);
    }
}

复杂度分析： 循环执行了 n/2 次。n/2 与 n 是同量级的，所以时间复杂度仍然是 O(n)。

if 和 for 的组合

在实际代码中,if 和 for 经常组合使用，这时需要综合分析。

示例：在嵌套循环中使用 if 提前终止

public boolean findInMatrix(int[][] matrix, int target) {
    // 假设 matrix 是一个 M x N 的矩阵
    int M = matrix.length;
    int N = matrix[0].length;
    // 外层循环 M 次
    for (int i = 0; i < M; i++) {
        // 内层循环 N 次
        for (int j = 0; j < N; j++) {
            // if 语句是 O(1)
            if (matrix[i][j] == target) {
                return true; // 找到后立即返回
            }
        }
    }
    return false;
}

复杂度分析：

• 最坏情况：目标元素不存在，或者藏在最后一个位置，外层循环 M 次，内层循环 N 次，总操作次数为 M * N，时间复杂度为 *`O(M N)** 或 **O(n²)`**（M=N=n）。
• 最好情况：目标元素在 [0][0] 位置。if 条件为真，只执行一次，时间复杂度为 O(1)。
• 平均情况：同样，我们通常关注最坏情况，所以复杂度是 O(M * N)。

这里的 if 语句起到了优化（提前返回）的作用，但没有改变最坏情况下的复杂度量级。

总结与表格

如何在实践中分析？

1. 识别输入规模 n：你的算法的输入是什么？数组大小？字符串长度？图中的节点数？这个 n 就是你分析的基础。
2. 计算基本操作次数：估算随着 n 的增长，算法中核心操作（如比较、赋值、算术运算）被执行的总次数。
3. 关注主导项：如果一个算法的复杂度是 O(3n² + 10n + 100)，n² 是主导项，当 n 很大时，3n² 的影响远超其他项，最终复杂度是 O(n²)。
4. 分析嵌套结构：从最内层开始，向外分析，每次遇到一层新的循环，就将当前的复杂度乘以 n。
5. 考虑 if 的影响：if 主要是流程控制，如果它不改变循环次数，就可以忽略其对量级的影响，如果它决定了一个主要代码块是否执行，就要分析两种情况下的复杂度。

掌握 if 和 for 对复杂度的影响是学习算法和数据结构的第一步，也是写出高性能代码的关键。