0-1背包问题的动态规划解法(Java实现)
0-1背包问题是动态规划中的经典问题,下面我将提供一个完整的Java实现,包括问题解释、动态规划思路和代码实现。
问题描述
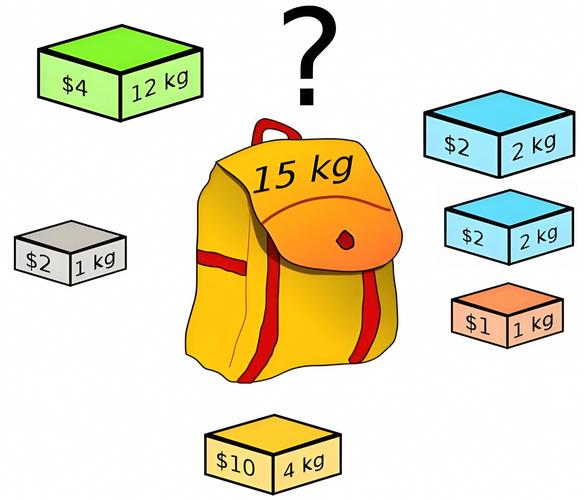
给定n个物品和一个容量为W的背包,第i个物品的重量是weight[i],价值是value[i],每个物品只能选择一次(0-1选择),如何选择物品使得装入背包的物品总价值最大?
动态规划思路
-
定义状态:
dp[i][w]表示前i个物品在容量为w的背包中的最大价值。 -
状态转移方程:
- 如果不选择第i个物品:
dp[i][w] = dp[i-1][w] - 如果选择第i个物品(前提是w >= weight[i-1]):
dp[i][w] = dp[i-1][w-weight[i-1]] + value[i-1] - 取两者最大值:
dp[i][w] = max(dp[i-1][w], dp[i-1][w-weight[i-1]] + value[i-1])
- 如果不选择第i个物品:
-
初始化:
dp[0][w] = 0(没有物品时价值为0),dp[i][0] = 0(容量为0时价值为0) (图片来源网络,侵删)
(图片来源网络,侵删)
Java实现
public class Knapsack01 {
/**
* 0-1背包问题动态规划解法
* @param weight 物品重量数组
* @param value 物品价值数组
* @param capacity 背包容量
* @return 最大价值
*/
public static int knapsack(int[] weight, int[] value, int capacity) {
int n = weight.length;
// 创建dp数组,dp[i][w]表示前i个物品在容量为w的背包中的最大价值
int[][] dp = new int[n + 1][capacity + 1];
// 初始化dp数组
for (int i = 0; i <= n; i++) {
dp[i][0] = 0; // 容量为0时价值为0
}
for (int w = 0; w <= capacity; w++) {
dp[0][w] = 0; // 没有物品时价值为0
}
// 填充dp数组
for (int i = 1; i <= n; i++) {
for (int w = 1; w <= capacity; w++) {
// 如果当前物品重量大于当前背包容量,则不能选择
if (weight[i - 1] > w) {
dp[i][w] = dp[i - 1][w];
} else {
// 选择或不选择当前物品,取最大值
dp[i][w] = Math.max(
dp[i - 1][w],
dp[i - 1][w - weight[i - 1]] + value[i - 1]
);
}
}
}
return dp[n][capacity];
}
public static void main(String[] args) {
int[] weight = {1, 3, 4, 5};
int[] value = {1, 4, 5, 7};
int capacity = 7;
int maxValue = knapsack(weight, value, capacity);
System.out.println("最大价值: " + maxValue); // 输出: 9 (选择物品2和3)
}
}
空间优化版本
我们可以将空间复杂度从O(n*W)优化到O(W),因为每次计算只依赖上一行的数据。
public class Knapsack01Optimized {
public static int knapsack(int[] weight, int[] value, int capacity) {
int n = weight.length;
int[] dp = new int[capacity + 1];
for (int i = 0; i < n; i++) {
// 从后向前更新,避免覆盖还未使用的上一轮数据
for (int w = capacity; w >= weight[i]; w--) {
dp[w] = Math.max(dp[w], dp[w - weight[i]] + value[i]);
}
}
return dp[capacity];
}
public static void main(String[] args) {
int[] weight = {1, 3, 4, 5};
int[] value = {1, 4, 5, 7};
int capacity = 7;
int maxValue = knapsack(weight, value, capacity);
System.out.println("最大价值: " + maxValue); // 输出: 9
}
}
复杂度分析
- 时间复杂度:O(n*W),其中n是物品数量,W是背包容量
- 空间复杂度:
- 原始版本:O(n*W)
- 优化版本:O(W)
这个动态规划解法能够高效地解决0-1背包问题,特别适合物品数量和背包容量不是特别大的情况。