Java 计算最大公约数(GCD)和最小公倍数(LCM)
在 Java 中,有几种方法可以计算两个数的最大公约数(Greatest Common Divisor, GCD)和最小公倍数(Least Common Multiple, LCM)。
使用欧几里得算法(辗转相除法)
欧几里得算法是计算 GCD 的高效方法,基于以下原理:
- GCD(a, b) = GCD(b, a % b)
- 当 b 为 0 时,GCD a
public class GCDAndLCM {
// 计算最大公约数(GCD)
public static int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
// 计算最小公倍数(LCM)
public static int lcm(int a, int b) {
return a * b / gcd(a, b);
}
public static void main(String[] args) {
int num1 = 12;
int num2 = 18;
System.out.println("GCD of " + num1 + " and " + num2 + " is: " + gcd(num1, num2));
System.out.println("LCM of " + num1 + " and " + num2 + " is: " + lcm(num1, num2));
}
}
使用 Java 8 的 Math 类(Java 9+)
从 Java 9 开始,java.lang.Math 类提供了 gcd() 方法:
public class GCDAndLCM {
// 计算最大公约数(使用Java 9+的Math.gcd)
public static int gcd(int a, int b) {
return Math.gcd(a, b);
}
// 计算最小公倍数
public static int lcm(int a, int b) {
return a * b / gcd(a, b);
}
public static void main(String[] args) {
int num1 = 12;
int num2 = 18;
System.out.println("GCD of " + num1 + " and " + num2 + " is: " + gcd(num1, num2));
System.out.println("LCM of " + num1 + " more than two numbers" + num2 + " is: " + lcm(num1, num2));
}
}
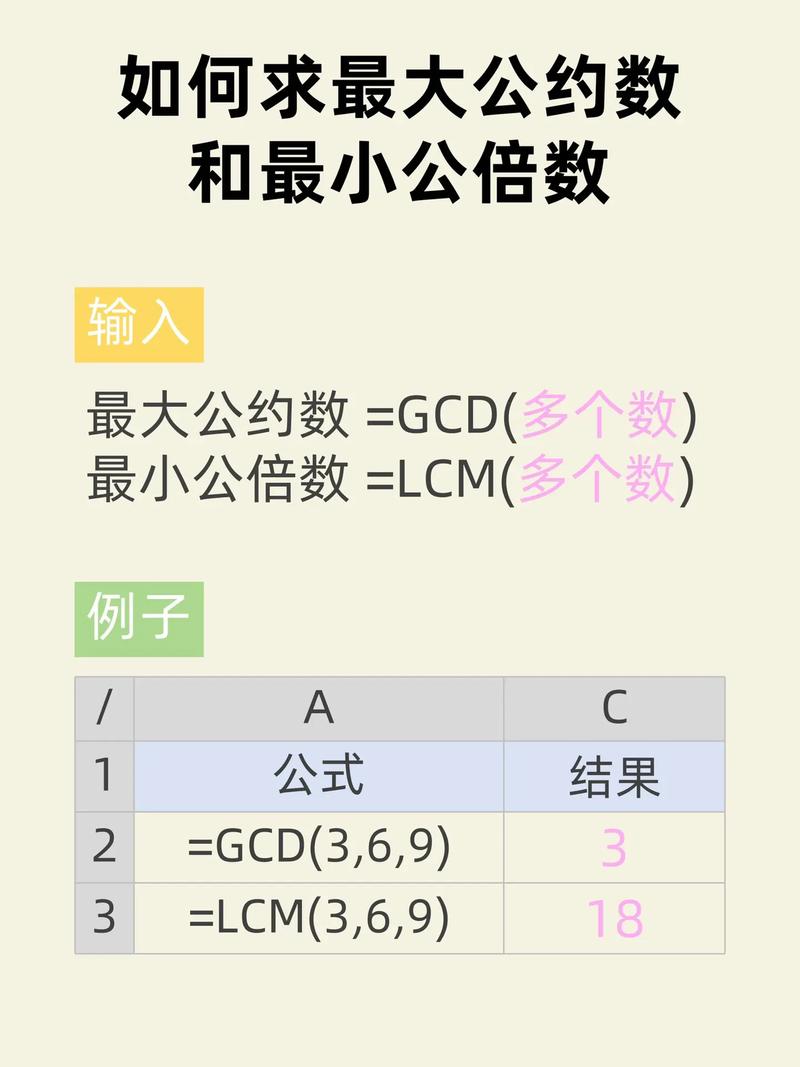
处理多个数的 GCD 和 LCM
如果要计算多个数的 GCD 和 LCM,可以依次计算:
import java.util.Arrays;
import java.util.Collections;
import java.util.List;
public class GCDAndLCM {
public static int gcd(int a, int b) {
if (b == 0) {
return a;
}
return gcd(b, a % b);
}
public static int lcm(int a, int b) {
return a * b / gcd(a, b);
}
// 计算多个数的GCD
public static int gcdOfList(List<Integer> numbers) {
return numbers.stream()
.reduce(0, (a, b) -> gcd(a, b));
}
// 计算多个数的LCM
public static int lcmOfList(List<Integer> numbers) {
return numbers.stream()
.reduce(1, (a, b) -> lcm(a, b));
}
public static void main(String[] args) {
List<Integer> numbers = Arrays.asList(12, 18, 24);
System.out.println("GCD of " + numbers + " is: " + gcdOfList(numbers));
System.out.println("LCM of " + numbers + " is: " + lcmOfList(numbers));
}
}
注意事项
-
处理负数时,GCD 结果始终为正数,可以在计算前取绝对值:
 (图片来源网络,侵删)
(图片来源网络,侵删)public static int gcd(int a, int b) { a = Math.abs(a); b = Math.abs(b); // 其余代码不变 } -
处理大数时,可以使用
BigInteger类:import java.math.BigInteger; public static BigInteger gcdBigInteger(BigInteger a, BigInteger b) { return a.gcd(b); } -
对于 LCM 计算,确保
a * b不会溢出,可以先进行除法:public static int lcm(int a, int b) { return (a / gcd(a, b)) * b; }
这些方法提供了在 Java 中计算 GCD 和 LCM 的不同方式,可以根据具体需求选择最适合的实现。