0-1背包问题的动态规划Java实现

0-1背包问题是经典的动态规划问题，其特点是每个物品要么被选择（放入背包），要么不被选择，不能部分选择。

问题描述

给定n个物品和一个容量为C的背包,第i个物品的重量是w[i]，价值是v[i]，如何选择装入背包的物品，使得装入背包中物品的总价值最大？

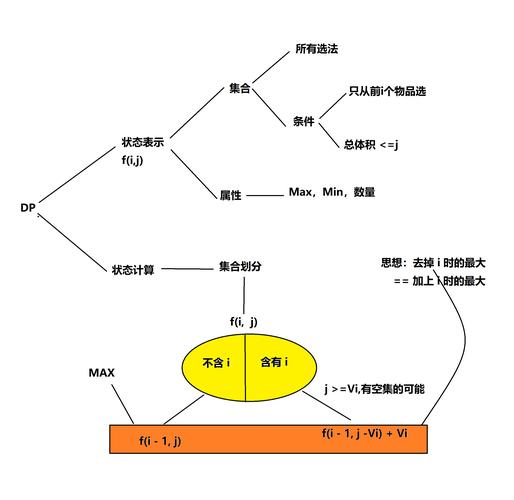
动态规划解法

二维DP数组

public class Knapsack01 {
    public static int knapsack(int[] weights, int[] values, int capacity) {
        int n = weights.length;
        // dp[i][j] 表示前i个物品在容量为j的背包中的最大价值
        int[][] dp = new int[n + 1][capacity + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= capacity; j++) {
                if (weights[i - 1] > j) {
                    // 当前物品重量大于背包容量，不能放入
                    dp[i][j] = dp[i - 1][j];
                } else {
                    // 选择放入或不放入当前物品，取最大值
                    dp[i][j] = Math.max(
                        dp[i - 1][j], 
                        dp[i - 1][j - weights[i - 1]] + values[i - 1]
                    );
                }
            }
        }
        return dp[n][capacity];
    }
    public static void main(String[] args) {
        int[] weights = {2, 3, 4, 5};
        int[] values = {3, 4, 5, 6};
        int capacity = 5;
        int maxValue = knapsack(weights, values, capacity);
        System.out.println("最大价值: " + maxValue); // 输出: 7
    }
}

空间优化的DP数组（一维数组）

public class Knapsack01Optimized {
    public static int knapsack(int[] weights, int[] values, int capacity) {
        int n = weights.length;
        // dp[j] 表示容量为j的背包中的最大价值
        int[] dp = new int[capacity + 1];
        for (int i = 0; i < n; i++) {
            // 从后向前遍历，避免重复计算
            for (int j = capacity; j >= weights[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - weights[i]] + values[i]);
            }
        }
        return dp[capacity];
    }
    public static void main(String[] args) {
        int[] weights = {2, 3, 4, 5};
        int[] values = {3, 4, 5, 6};
        int capacity = 5;
        int maxValue = knapsack(weights, values, capacity);
        System.out.println("最大价值: " + maxValue); // 输出: 7
    }
}

算法分析

1. 时间复杂度：O(n*C)，其中n是物品数量，C是背包容量
2. 空间复杂度：
   • 二维DP数组：O(n*C)
   • 一维DP数组：O(C)

关键点说明

1. 状态定义：dp[i][j]表示前i个物品在容量为j的背包中的最大价值
2. 状态转移方程：
   • 如果第i个物品不能放入（重量>剩余容量）：dp[i][j] = dp[i-1][j]
   • 否则：dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])
3. 空间优化：使用一维数组时，需要从后向前遍历，避免覆盖还未计算的值

扩展问题

如果需要知道具体选择了哪些物品,可以在DP过程中记录选择状态：

public class Knapsack01WithItems {
    public static void knapsackWithItems(int[] weights, int[] values, int capacity) {
        int n = weights.length;
        int[][] dp = new int[n + 1][capacity + 1];
        boolean[][] selected = new boolean[n + 1][capacity + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= capacity; j++) {
                if (weights[i - 1] > j) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    int valueWith = dp[i - 1][j - weights[i - 1]] + values[i - 1];
                    if (valueWith > dp[i - 1][j]) {
                        dp[i][j] = valueWith;
                        selected[i][j] = true;
                    } else {
                        dp[i][j] = dp[i - 1][j];
                    }
                }
            }
        }
        System.out.println("最大价值: " + dp[n][capacity]);
        // 回溯选择的物品
        int j = capacity;
        for (int i = n; i > 0; i--) {
            if (selected[i][j]) {
                System.out.println("选择了物品 " + i + " (重量: " + weights[i-1] + ", 价值: " + values[i-1] + ")");
                j -= weights[i - 1];
            }
        }
    }
    public static void main(String[] args) {
        int[] weights = {2, 3, 4, 5};
        int[] values = {3, 4, 5, 6};
        int capacity = 5;
        knapsackWithItems(weights, values, capacity);
    }
}

这个实现不仅能计算最大价值,还能输出具体选择了哪些物品。